testing out t-tests
September 8, 2018
I was trying to work out how to do t-tests using my own data and the lsr package but ended up working with Dani’s AFL data from her book while trying to work out why R insisted that my outcome variable wasn’t numeric (it definitely was). Turns out that the lsr package doesn’t deal well with tibbles (which are created by default when you use read_csv to get your data) but if you use read.csv or specify as.dataframe, it works beautifully (and produces much more digestable output than the t.test function).
Take home message.
Here is what I learned about t-tests from doing the analysis below.
From the lsr package
I like that the lsr has separate functions for each kind of t-test. I can see how that will make it easier for students to think about the differences between each test, and the arguments that each one requires.
The output from the lsr is also REALLY nice. It includes useful things like Cohens D by default. Important to make sure you are working with a dataframe though. The code is old and doesn’t deal with tibbles.
Code for one sample, paired, and independent samples t-tests using lsr
oneSampleTTest(dataframe$testcolumn, mu=100)
pairedSamplesTTest(~ variable1 + variable2, dataframe) #note if data is long you also need to specify "id"
independentSamplesTTest(outcome ~ group, dataframe)
Code for doing the same thing using the standard t.test method
t.test(dataframe$testcolumn, mu = 100)
t.test(dataframe$variable1, dataframe$variable2, paired=TRUE)
t.test(dataframe$outcome ~ dataframe$group, paired=FALSE)
Analysing the AFL data
The AFL data that comes with Dani’s book includes attendance and score information for home and away teams over regular and finals games for years and years. Disclaimer- I know nothing about AFL.
Load packages
library(tidyverse)
## ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.1 ──
## ✓ ggplot2 3.3.5 ✓ purrr 0.3.4
## ✓ tibble 3.1.6 ✓ dplyr 1.0.7
## ✓ tidyr 1.1.4 ✓ stringr 1.4.0
## ✓ readr 2.1.1 ✓ forcats 0.5.1
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag() masks stats::lag()
library(lsr)
Read the data
Remember: lsr package does not like tibbles. Best to use read.csv or as.dataframe to make sure you are working with a df.
afl <- read.csv("afl.csv")
homeawaygames <- afl %>%
select(home_score, away_score, game_type, attendance)
names(homeawaygames)
## [1] "home_score" "away_score" "game_type" "attendance"
AFL data questions
Question 1: does the home team score more than 100 points on average each game?
Maybe we know that the average AFL team scores around 100 points in a game. Do home teams score more than 100?
The lsr one sample t test
oneSampleTTest(homeawaygames$home_score, mu=100)
##
## One sample t-test
##
## Data variable: homeawaygames$home_score
##
## Descriptive statistics:
## home_score
## mean 101.508
## std dev. 29.660
##
## Hypotheses:
## null: population mean equals 100
## alternative: population mean not equal to 100
##
## Test results:
## t-statistic: 3.333
## degrees of freedom: 4295
## p-value: <.001
##
## Other information:
## two-sided 95% confidence interval: [100.621, 102.396]
## estimated effect size (Cohen's d): 0.051
Interesting, on average yes, the home team does score more than 100. What about the away team?
oneSampleTTest(homeawaygames$away_score, mu=100)
##
## One sample t-test
##
## Data variable: homeawaygames$away_score
##
## Descriptive statistics:
## away_score
## mean 91.119
## std dev. 29.027
##
## Hypotheses:
## null: population mean equals 100
## alternative: population mean not equal to 100
##
## Test results:
## t-statistic: -20.054
## degrees of freedom: 4295
## p-value: <.001
##
## Other information:
## two-sided 95% confidence interval: [90.251, 91.987]
## estimated effect size (Cohen's d): 0.306
Also significant, but this was a 2 sided test, so this significant result tells us that on average the away team scores significantly less than 100 points.
The t.test one sample t test
The format is mostly the same for the t.test version; output not as nice.
t.test(homeawaygames$home_score, mu = 100)
##
## One Sample t-test
##
## data: homeawaygames$home_score
## t = 3.3333, df = 4295, p-value = 0.0008654
## alternative hypothesis: true mean is not equal to 100
## 95 percent confidence interval:
## 100.6212 102.3955
## sample estimates:
## mean of x
## 101.5084
t.test(homeawaygames$away_score, mu = 100)
##
## One Sample t-test
##
## data: homeawaygames$away_score
## t = -20.054, df = 4295, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 100
## 95 percent confidence interval:
## 90.2507 91.9872
## sample estimates:
## mean of x
## 91.11895
Question 2- do teams playing at home score more than teams playing away?
In the afl dataset, each game (like participant) gives a score for the home team and the away team. In that sense the score data is paired.
The lsr paired samples t test
The lsr package pairedSamplesTest() function looks a bit different if the data is wide vs long. If the data is wide, you need to just tell in the names of the variables to compare and the data set.
WideTest <- pairedSamplesTTest(
formula = ~ variable1 + variable2,
data = dataframe
)
If the data is long, you also need to tell it the ‘ID’ column.
LongTest <- pairedSamplesTTest(
formula = ~ variable1 + variable2,
data = dataframe,
id = "id"
)
Paired samples t test the lsr way (longform)
pairedSamplesTTest(
formula = ~ home_score + away_score,
data = homeawaygames
)
##
## Paired samples t-test
##
## Variables: home_score , away_score
##
## Descriptive statistics:
## home_score away_score difference
## mean 101.508 91.119 10.389
## std dev. 29.660 29.027 44.335
##
## Hypotheses:
## null: population means equal for both measurements
## alternative: different population means for each measurement
##
## Test results:
## t-statistic: 15.359
## degrees of freedom: 4295
## p-value: <.001
##
## Other information:
## two-sided 95% confidence interval: [9.063, 11.716]
## estimated effect size (Cohen's d): 0.234
Paired samples t test the lsr way (shortform)
pairedSamplesTTest(~ home_score + away_score, homeawaygames)
##
## Paired samples t-test
##
## Variables: home_score , away_score
##
## Descriptive statistics:
## home_score away_score difference
## mean 101.508 91.119 10.389
## std dev. 29.660 29.027 44.335
##
## Hypotheses:
## null: population means equal for both measurements
## alternative: different population means for each measurement
##
## Test results:
## t-statistic: 15.359
## degrees of freedom: 4295
## p-value: <.001
##
## Other information:
## two-sided 95% confidence interval: [9.063, 11.716]
## estimated effect size (Cohen's d): 0.234
Take home message, home teams score more points that away teams.
The t.test paired samples t test
Alternatively the basic t.test function does the same with less digestable output.
t.test(y1, y2, paired=TRUE)
t.test(homeawaygames$home_score, homeawaygames$away_score, paired=TRUE)
##
## Paired t-test
##
## data: homeawaygames$home_score and homeawaygames$away_score
## t = 15.359, df = 4295, p-value < 2.2e-16
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 9.063302 11.715562
## sample estimates:
## mean of the differences
## 10.38943
t.test output definitely not as nice.
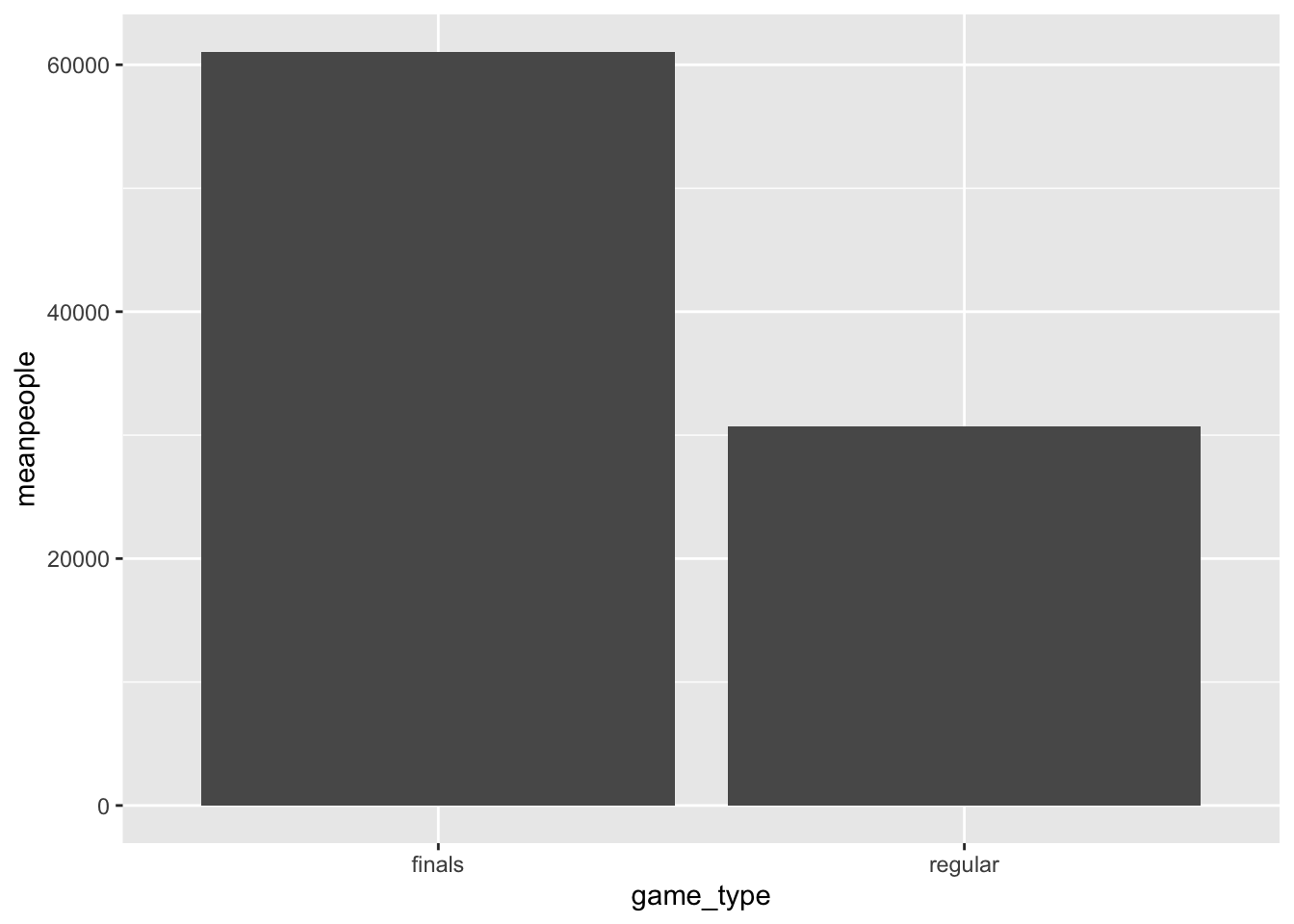
Question 3: Is attendance higher at finals games than regular season games?
Lets group by game type and calculate the mean number of people attending finals vs regular games. Seems like attendance is higher for finals. Is that significant?
homeawaygames %>%
group_by(game_type) %>%
summarise(meanpeople = mean(attendance)) %>%
ggplot(aes(x = game_type, y= meanpeople)) +
geom_col()
The lsr independent samples t test
R t-test uses the Welch method (for unequal variance) by default. Need to change var.equal = TRUE to use Student t-test method.
independentSamplesTTest(
formula = outcome ~ group,
data = dataframe
var.equal = FALSE
)
Independent samples t test the lsr way (longform)
independentSamplesTTest(
formula = attendance ~ game_type,
data = homeawaygames,
var.equal = FALSE
)
## Warning in independentSamplesTTest(formula = attendance ~ game_type, data =
## homeawaygames, : group variable is not a factor
##
## Welch's independent samples t-test
##
## Outcome variable: attendance
## Grouping variable: game_type
##
## Descriptive statistics:
## finals regular
## mean 61054.950 30681.175
## std dev. 20950.884 15044.015
##
## Hypotheses:
## null: population means equal for both groups
## alternative: different population means in each group
##
## Test results:
## t-statistic: 20.249
## degrees of freedom: 209.14
## p-value: <.001
##
## Other information:
## two-sided 95% confidence interval: [27416.749, 33330.801]
## estimated effect size (Cohen's d): 1.665
Independent samples t test the lsr way (shortform)
independentSamplesTTest(attendance ~ game_type, homeawaygames)
## Warning in independentSamplesTTest(attendance ~ game_type, homeawaygames): group
## variable is not a factor
##
## Welch's independent samples t-test
##
## Outcome variable: attendance
## Grouping variable: game_type
##
## Descriptive statistics:
## finals regular
## mean 61054.950 30681.175
## std dev. 20950.884 15044.015
##
## Hypotheses:
## null: population means equal for both groups
## alternative: different population means in each group
##
## Test results:
## t-statistic: 20.249
## degrees of freedom: 209.14
## p-value: <.001
##
## Other information:
## two-sided 95% confidence interval: [27416.749, 33330.801]
## estimated effect size (Cohen's d): 1.665
The t.test independent samples t test
Alternatively the basic t.test function does the same with less digestable output. y1 = outcome, y= group.
t.test(y1 ~ y2, paired=FALSE)
t.test(homeawaygames$attendance ~ homeawaygames$game_type, paired=FALSE, var.equal = FALSE)
##
## Welch Two Sample t-test
##
## data: homeawaygames$attendance by homeawaygames$game_type
## t = 20.249, df = 209.14, p-value < 2.2e-16
## alternative hypothesis: true difference in means between group finals and group regular is not equal to 0
## 95 percent confidence interval:
## 27416.75 33330.80
## sample estimates:
## mean in group finals mean in group regular
## 61054.95 30681.18